ارائه و تحلیل داده های مربوط به مدیریت پسماند

ارائه و تحلیل داده های مربوط به مدیریت پسماند

فرمت: PDF   تعداد صفحات: 16

فهرست:

• فنون مورد استفاده برای ارائه ترسیمی و تحلیل داده های مربوط به مدیریت پسماند
• روش های آماری که به طور معمول برای مشخص کردن نرخ های جمع آوری پسماند مورد استفاده قرار می گیرند
• روش های ترسیمی که می تواند برای مشخص کردن ماهیت یک توزیع مورد استفاده واقع شود.

ارائه ترسیمی داده های میدانی

ارائه ترسیمی داده هایی که از کارهای میدانی به دست آمده اند را می توان برای تشریح و مشخص سازی روند و گرایش منطقی بین داده ها مورد استفاده قرار داد. سری های زمانی و نمودار ستونی یا نمودارهای فراوانی، به طور وسیعی برای ارائه و تحلیل این قبیل داده ها استفاده می شوند.

سری های زمانی

مشاهداتی که بر مبنای زمان رخداد مرتب شده اند را غالبا سرهای زمانی می نامند. با رسم مقادیر مشاهده شده در مقابل زمان، اغلب درک روندها و گرایش ها، چرخه ها و نوسانات ارزشمند در فهم ماهیت پایه رخدادهای تحت ارزیابی، امکان پذیر می شود.

تشریح روند (گرایش ها)، چرخه ها و نوسانات. واژه روند برای تشریح گرایشی نسبتا طولانی مدت از مشاهدات میدانی در جهت افزایش یا کاهش در برخی از روش های منظم مورد استفاده قرار می گیرد (شکل ۱الف را ببینید). تغییر در مقادیر مشاهدات می تواند ساده و یا پیچیده باشد.

مشاهدات چرخ های به معنی حرکت داده ها به سمت بالا تا نقطه اوج و سپس فرود آنها تا کمترین مقدار، می باشد (شکل ۱ب را ببینید). مشابه روندها، چرخه ها نیز می توانند چرخ های ساده بوده یا ممکن است به صورت چرخه های تکراری طولانی مدت باشند.

اصطلاح سری های زمانی نوسانی اغلب برای تشریح مشاهداتی بکار می رود که تغییر معنی داری از یک فاصله زمانی تا فاصله بعدی بدون الگوی مشخصی در این مشاهدات دیده می شود (شکل ۱ج را ببینید).

تحلیل روندها، چرخه ها و نوسانات. از لحاظ ریاضی، روندهای خطی به صورت معادله خطی y = a + bx تشریح می شوند. روندهای منحنی‌وار بطور متداول به صورت معادله کلی y = a + bx + cx^۲ نشان داده می شوند، اگر چه بسیاری از معادله های دیگر نیز می توانند مورد استفاده قرار گیرند[1]. روش میانگین متحرک اغلب برای از بین بردن بی قاعدگی های تصادفی در رسم سرهای زمانی داده ها، به نحوی مورد استفاده قرار می گیرند که قادر به پوشش دادن روندهای کوتاه مدت و بلند مدت می باشند.

میانگین متحرک ممکن است ساده یا وزن دار باشد. میانگین متحرک با میانگین گیری و اضافه کردن تعداد مشاهدات متوالی به میانگین حاصله به دست می آید. بنابراین میانگین با میانه متناظر خواهد شد که می توان برای تأکید آن را وزن دار کرد. دو مثال از میانگین متحرک وزن دار با معادلات (۱) و (۲) نشان داده شده است.

معادله 1: X_b = ^_a+2b+c / ₄

که X_b = مقدار میانگین در نقطه b
c و b و a = حجم های مشاهده در نقاط a و b و c

 معادله 2: X_c = ^{_a+4b+6c+4d+e}/ ₁₆

ضرایب موجود در میانگین متحرک داده شده در معادله (۲) از توزیع دو جمله ای به دست می آیند. میانگین متحرک وزن دار برای سری های زمانی تناوبی نشان داده شده در شکل (۱ج) با استفاده از معادله (۱) محاسبه شده اند.

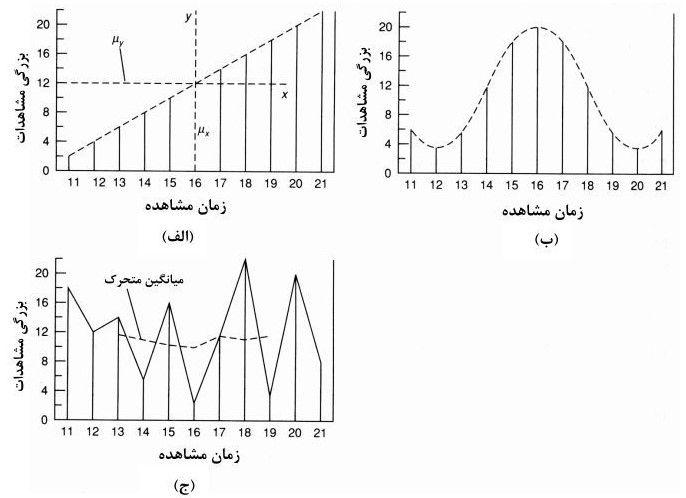
شکل ۱: نمودارهای سری های زمانی که معرف داده های سری های زمانی هستند که الف) از یک روند تبعیت می کنند ب) چرخه ای هستند ج) نوسانی می باشند (از منبع ۱).

توزیع فراوانی

مشاهدات از لحاظ تعداد به شکل ردیفی مرتب می شوند. داده های مشابه را می توان در یک سری از محدوده های داده ای، با هم جمع کرد. در صورتی که کل شماره ها نمایانگر تعداد مشاهداتی باشند که در هر بازه زمانی رخ می دهد، بنابراین فراوانی رخداد کل شماره ها را می توان در مقابل اندازه یا بزرگی بازه زمانی رسم کرد. نمودارهای حاصله نمودار ستونی نامیده میشوند (شکل ۲ را ببینید). همانطور که نشان داده شده است، این نمودارها می توانند متقارن (شکل ۲الف)، غیر متقارن (شکل ۲ب)، مستطیلی (۲ج) یا U- شکل (شکل ۲د) باشد. داده های تشکیل دهنده نمودارهای ستونی متقارن را دارای توزیع نرمال گویند و داده های نمودارهای ستونی نامتقارن را دارای توزیع چوله شده می نامند.

ادامه مطلب را با دانلود فایل پیوستی مشاهده کنید.

حتما بخوانید:

⇐ برنامه ریزی، مکان یابی و کسب مجوز برای تسهیلات مدیریت پسماند

⇐ اجرای برنامه های مدیریت پسماند

⇐ تعطیلی، احیا و بازسازی محل های دفن پسماند