آشنایی با روش های طراحی آزمایش ها در آزمایشگاه

آشنایی با روش های طراحی آزمایش ها در آزمایشگاه

فرمت: Pdf  تعداد صفحات: 88

فهرست:

• نحوه انتخاب بهترین طرح قبل از انجام طراحی آزمایش
• معرفی روش سطح پاسخ
  • طراحی به روش ترکیب مرکزی
  • طرح باکس – بنکن
  • ایجاد طرح باکس- بنکن با ۴ عامل (۴=k)
  • ایجاد طرح باکس – بنکن با ۵ عامل (۵=k)
• بهینه سازی در روش سطح پاسخ
• معرفی روش های عاملی
  • طرح یک متغیر در آن واحد (طرح یک عاملی)
  • طرح های چند عاملی (فاکتوریل)
  • طرح فاکتوریل دو سطحی (طرح عاملی با دو سطح یا 2²)
  • فاکتوریل سه عاملی و دو سطحی
  • تحلیل گرافیکی
  • تحلیل خطا
  • استفاده از نقطه مرکزی، در طرح فاکتوریل دو سطح
  • کاربرد استفاده از آماره t
  • اصلاح محاسبات بر اساس خطای باقیمانده
  • طرح فاکتوریل جزئی دو سطحی (2^k-p)
  • تشکیل جدول فاکتوریل جزئی با استفاده از جدول فاکتوریل کامل
  • مراحل طراحی آزمایش به روش فاکتوریل جزئی 2^k-p
  • طرح فاکتوریل با سه سطح (طرح عاملی سه یا 3^k)
  • طرح 3²
• طرح های مربعی
  • طرح مربع لاتین
  • طرح مربع لاتین یونانی
  • طرح مربع بودن
  • طرح پلاکت – برمن
  • طرح تاخورده پلاکت برمن
• معرفی روش D-Optimal
  • مجموعه کاندید
  • ماتریس طرح
  • معیار برای بهترین طرح D-Optimal
  • مدل درجه دوم
  • تعداد آزمایش های طرح D-Optimal
  • تحلیل خطا
• معرفی روش تاگوچی
  • مقدمه
  • تعریف ها
  • طراحی یک آرایه متعامد
  • چگونگی بررسی اثرهای متقابل در روش تاگوچی
  • مراحل اجرای یک طرح تاگوچی
  • تحلیل آماری و به دست آوردن شرایط بهینه

نحوه انتخاب بهترین طرح قبل از انجام طراحی آزمایش

در انجام طراحی آزمایش ها با استفاده از بسته نرم افزاری DOE، با توجه به ماهیت آزمایش و تعدد فاکتورها، پاسخ ها و انتظار محقق از نتیجه آزمایش ها، می توان از روش های مختلف موجود در این برنامه استفاده نمود. جهت استفاده و انتخاب درست یک یا چند روش از مجموع روش های موجود، آشنایی با انواع روش ها، اصول و قوانین ریاضیاتی و آماری که هر کدام از روش ها از آن تبعیت می کند، توانمندی ها و محدودیت روش ها برای طراحی آزمایش ها مناسب، خروجی های مورد انتظار محقق و نحوه ی استفاده از روش ها، در این بخش مورد بررسی قرار می گیرد.

با توجه به اهمیت آشنایی محققین با مهم ترین روش های مورد استفاده، به ویژه در زمینه مهندسی محیط زیست، مرور مطالب این بخش جهت بهره برداری و درک صحیح از نحوه ی استفاده از آنها در بخش های مختلف محیط زیست از جمله مدیریت پسماند، پاکسازی خاک، آب و فاضلاب و هوا، توصیه می گردد [۱].

معرفی روش سطح پاسخ

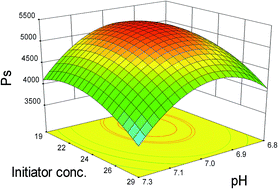
روش شناسی سطح پاسخ در دهه ۱۹۵۰ میلادی توسط Box و همکاران او پدید آمد. این اصطلاح، ریشه در دیدگاهی گرافیکی داشت که پس از برازش مدل های تجربی بر داده های آزمایشگاهی استوارند. بر اساس چنین هدفی، برای توصیف سیستم مورد نظر و در نهایت کشف و بهینه سازی شرایط آزمایشگاهی، از توابع خطی یا مرتبه دوم استفاده می شود.

برخی مراحل کاربردی روش سطح پاسخ (RSM) به عنوان تکنیک بهینه یابی، عبارت اند از:

1. انتخاب متغیرهایی با تأثیر چشم گیر بر سیستم (از طریق مطالعات غربال گری) و سپس تعیین حدود آزمایش مطابقت با هدف مطالعه و تجربه پژوهشگر
2. انتخاب طرح آزمایش و انجام آزمایش ها بنا بر ماتریس انتخابی
3. پردازش ریاضیاتی – آماری داده های به دست آمده با برازش یک تابع چند جمله ای
4. ارزیابی سازگاری مدل
5. بررسی لزوم و امکان جابجایی مسیر دست یافتن به ناحیه بهینه
6. به دست آوردن مقادیر بهینه هر متغیر.

روش RSM و مدل داده های موجود، شامل مجموعه تکنیک های آماری و ریاضی است که برای تعریف روابط بین «پاسخ» و متغیرهای مستقل به کار می رود. در این تکنیک، اثر متغیرهای مستقل روی یک فرآیند به تنهایی یا در ترکیب با یکدیگر بررسی می گردد. این روش آزمایشگاهی، علاوه بر آنالیز اثر متغیرهای مستقل، یک مدل ریاضیاتی تشکیل می دهد. در واقع، عبارت روش شناسی سطح پاسخ، اشاره به نمای گرافیکی سه بعدی به دست آمده از معادله ریاضی دارد. رابطه بین پاسخ و متغیرها به صورت معادله زیر است:

R = f(x₁,x₂,…,x_n) + ε

که در آن، R پاسخ، X متغیرهای مستقل و n تعداد متغیرهاست. ε خطای آماری ناشی از نوسان مواردی است که در ا لحاظ نشده اند. این موارد شامل تاثیراتی چون خطای اندازه گیری است. معمولا فرض می شود، ε توزیعی نرمال با میانگین و واریانس صفر دارد.

در روش سنتی طراحی آزمایش ها که همچنان کاربرد گسترده ای دارد (یک عامل در هر زمان)، تنها یک پارامتر تغییر می کند و سایر پارامترها ثابت نگه داشته می شود. مهم ترین نقطه ضعف این روش، عدم توجه به اثرات متقابل متغیرهای مورد مطالعه است. در نتیجه، این روش تصویر کاملی از اثرات متغیرها بر پاسخ ارائه نمی دهد. نقطه ضعف دیگر این روش، افزایش تعداد آزمایش های لازم برای تحقیقات مورد نظر است که زمان بر و پرهزینه بوده و افزایش مواد مصرفی را در پی دارد. به منظور بر طرف کردن این نقاط ضعف، بهینه سازی روش های تحلیلی با استفاده از تکنیک های آماری چند متغیره صورت می گیرد که از میان آنها Historical Data مناسب ترین روش است. این روش را می توان برای دریافت پاسخ یا مجموعه پاسخ، توسط چندین متغیر نیز به کار برد. در واقع هدف از به کار گیری Historical Data، مدل سازی داده های موجود و بهینه سازی همزمان سطوح متغیرها برای رسیدن به بهترین عملکرد سیستم است.

ساده ترین مدل به کار رفته در Historical Data، بر مبنای تابع خطی است. بدین منظور، ضروری است معادله زیر به خوبی جوابگوی «پاسخ» باشد:

y = β₀∑^K₁ β_i x_i + ε

که در آن، k تعداد متغیرها، β₀ ثابت، β_i ضرایب پارامترهای خطی، x_i متغیرها و ε مقدار باقیمانده هر آزمایش است.

به علت آنکه معادله فوق از مرتبه اول است، پاسخ ها هیچ گونه خمیدگی ندارد. به منظور تخمین اثرات مرتبه اول، طراحی دو سطحی به کار می رود. برای لحاظ کردن خمیدگی، به مدلی با مرتبه دوم نیاز است و در حالتی که اثرات جانبی در پاسخ دخیل اند، اثرات مرتبه دوم اهمیت می یابند. به

منظور گنجاندن خمیدگی، یک نقطه مرکزی در طراحی فاکتوریل در نظر گرفته می شود. بنابراین در مرحله بعد مدل چند جمله ای، عباراتی دیگر به نشانه اندر کنش ها، افزوده می شوند و مدل مرتبه دوم به صورت زیر در می آید:

 y = β₀∑^K₁ β_i x_i + ∑^K₁ β_ij x_ix_j + ε

که در آن، β_ij نشانگر ضرایب پارامترهای اندر کنشی است.

علاوه بر عبارات فوق، برای تعیین نقطه های بحرانی (ماکزیمم، مینیمم، یا زینی شکل)، بایستی عبارات مرتبه دوم به چند جمله ای فوق افزوده شود:

y = β₀∑^K₁ β_i x_i +∑^K₁ β_ii x_i² + ∑^K₁ β_ij x_ix_j + ε

که در آن، β_ii نشانگر ضرایب پارامتر مرتبه دوم است. به منظور تخمین پارامترها در معادله فوق، باید اطمینان یافت که تمامی متغیرها، حداقل در سه سطح مختلف تحت بررسی قرار گیرند.

پس از کسب داده های مربوط به هر نقطه در محدوده آزمایش، ضروری است معادل های ریاضی به منظور توصیف رفتار پاسخ برای داده ها، در نظر گرفته شود. به بیان دیگر، برآوردی تقریبی از پارامترهای ما، در معادلات به دست می آید. بنابراین می توان معادلات را به صورت ماتریسی در رابطه زیر نشان داد:

y_mx_i = X_mx_nb_nx_j + e_mx_j;

که در آن، لا پاسخ، X ماتریس نقاط انتخابی آزمایشی، b بردار پارامترهای مدل، e باقیمانده، m و n به ترتیب تعداد سطر و ستون ماتریس ها است.

معادله فوق با روشی آماری تحت عنوان روش حداقل مربعات، حل می شود. این روش، یک تکنیک رگرسیون چندگانه است که از طریق آن، یک مدل ریاضی به مجموعه داده ها نسبت داده می شود. معادله به نحوی تعیین می گردد که حداقل باقیمانده ممکن به دست آید. پس از تبدیل ریاضی ماتریس ها، می توان بردار b را به دست آورد تا ضرایب b با کمترین محاسبات ممکن به دست آید. در روش حداقل مربعات، فرض بر این است که توزیع خطاها تصادفی و میانگین خطاها صفر است و خطاها مستقل از یکدیگر هستند. بنابراین واریانس در مؤلفه های بردار b را می توان از تکرار در نقطه مرکزی به دست آورد:

V(b)_n = (X^T_nmX_m.n)^-1S²

با گرفتن مجذور هر مؤلفه بردار (b)، میزان خطای استاندارد ضرایب b در معادله «سطح پاسخ» حاصل می گردد.

پس از تعیین متغیرهایی که بر پاسخ فرآیند موثر هستند، مرحله بعد بهینه یابی فرآیند است. یعنی تعیین بازه ای از متغیرهای مهم که منجر به مطلوب ترین پاسخ شوند. به عبارت دیگر، بهینه یابی به معنای یافتن مناسب ترین شرایط از نظر ترکیب عوامل موثر در یک فرآیند خواهد بود. برای بهینه یابی یک سیستم، می بایست معادله پاسخ معلوم گردد و پاسخ این معادله، به طور تجربی تعیین گردد.

ادامه مطلب را با دانلود فایل پیوستی مشاهده کنید.

حتما بخوانید:

⇐ ایمنی و بهداشت در آزمایشگاه های آب و فاضلاب

⇐ آشنایی با روش های محلول سازی در آزمایشگاه

⇐ روش های کنترل کیفی و کالیبراسیون تجهیزات آزمایشگاهی